1.104.653
kiadvánnyal nyújtjuk Magyarország legnagyobb antikvár könyv-kínálatát

VISSZA
A TETEJÉRE
JAVASLATOKÉszre-
vételek
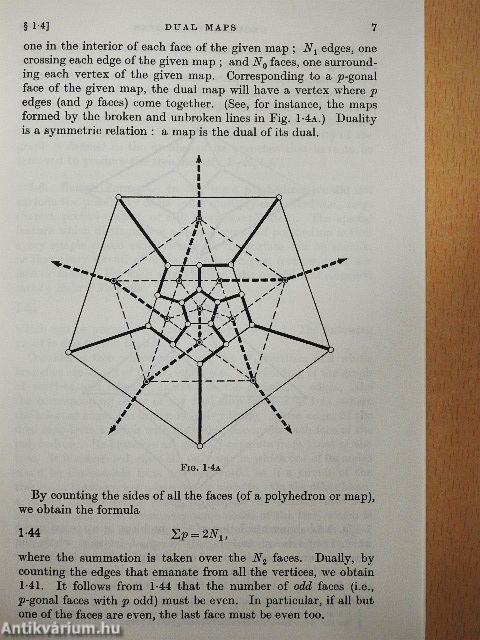
Regular Polytopes
| Kiadó: | Dover Publications, Inc. |
|---|---|
| Kiadás helye: | New York |
| Kiadás éve: | |
| Kötés típusa: | Ragasztott papírkötés |
| Oldalszám: | 321 oldal |
| Sorozatcím: | |
| Kötetszám: | |
| Nyelv: | Angol |
| Méret: | 22 cm x 14 cm |
| ISBN: | |
| Megjegyzés: | 3. kiadás. Fekete-fehér ábrákkal, fotókkal. |
naponta értesítjük a beérkező friss
kiadványokról
naponta értesítjük a beérkező friss
kiadványokról
Előszó
TovábbFülszöveg
REGULAR POLYTOPES
H.S.m. Gsxeter
Polytdpes are geometrical figures bounded by portions of lines, planes or hyperplanes. In plane (two dimensional) geometry they are known as polygons and comprise such figures as triangles, squares, pentagons, etc. In solid (three dimensional) geometry they are known as polyhedra and include such figures as tetrahedra (a type of pyramid), cuKes, icosahedra and many more; the possibilities, in fact, are infinite! H. S. M. Coxeter's book is the foremost book available on regular polyhedra, incorporating not only the ancient Greek work on the subject, but also the vast amount of information that has been accumulated on them since, especially in the last hundred years. The author, professor of Mathematics, University of Toronto, has contributed much valuable work himself on polytopes and is a well known authority on them.
Professor Coxeter begins with the fundamental concepts of plane and solid geometry and then moves on to multi-dimensionality.... Tovább
Fülszöveg
REGULAR POLYTOPES
H.S.m. Gsxeter
Polytdpes are geometrical figures bounded by portions of lines, planes or hyperplanes. In plane (two dimensional) geometry they are known as polygons and comprise such figures as triangles, squares, pentagons, etc. In solid (three dimensional) geometry they are known as polyhedra and include such figures as tetrahedra (a type of pyramid), cuKes, icosahedra and many more; the possibilities, in fact, are infinite! H. S. M. Coxeter's book is the foremost book available on regular polyhedra, incorporating not only the ancient Greek work on the subject, but also the vast amount of information that has been accumulated on them since, especially in the last hundred years. The author, professor of Mathematics, University of Toronto, has contributed much valuable work himself on polytopes and is a well known authority on them.
Professor Coxeter begins with the fundamental concepts of plane and solid geometry and then moves on to multi-dimensionality. Among the many subjects covered are Euler's formula, rotation groups, star-polyhedra, truncation, forms, vectors, coordinates, kaleidoscopes, Petrig polygons, sections and projections, and star-polytopes. Each chapter ends with a historical summary showing when and how the information contained therein was discovered. Numerous figures and examples and the author's lucid explanations also help to make the text readily comprehensible.
Although the study of polytopes does have some practical applications to mineralogy, architecture, linear programming and other areas, most people enjoy contemplating these figures simply because their symmetrical shapes have an aesthetic appeal. But whatever the reasons, anyone with an elementary knowledge of geometry and trigonometry will find this one of the best source books available on this fascinating study.
Unabridged, corrected republication of the second (1963) edition. A new Preface by the author. Definitions of symbols. 8 tables. Bibliography. Index. 8 plates plus numerous diagrams and examples, xiv + 321pp. 5% x 8)2. Paperbound.
A DOVER EDITION DESIGNED FOR YEARS OF USE!
We have made every effort to make this the best book possible. Our paper is opaque, with minimal show-through; it will not discolor or become brittle with age. Pages are bound in signatures, in the method traditionally used for the best books, and will not drop out. Books open flat for easy reference. The binding will not crack or split. This is a permanent book. Vissza
Témakörök
H. S. M. Coxeter
H. S. M. Coxeter műveinek az Antikvarium.hu-n kapható vagy előjegyezhető listáját itt tekintheti meg: H. S. M. Coxeter könyvek, művekMegvásárolható példányok
Nincs megvásárolható példány
A könyv összes megrendelhető példánya elfogyott. Ha kívánja, előjegyezheti a könyvet, és amint a könyv egy újabb példánya elérhető lesz, értesítjük.